浮点标准 IEEE754 精要
(→半精度浮点) |
(→半精度浮点) |
||
| 第47行: | 第47行: | ||
exponent 为指数位,有 5 位长: | exponent 为指数位,有 5 位长: | ||
| − | + | The half-precision binary floating-point exponent is encoded using an offset-binary representation, with the zero offset being 15; also known as exponent bias in the IEEE 754 standard. | |
| + | * Emin = 000012 − 011112 = −14 | ||
| + | * Emax = 111102 − 011112 = 15 | ||
| + | * Exponent bias = 011112 = 15 | ||
| − | + | Thus, as defined by the offset binary representation, in order to get the true exponent the offset of 15 has to be subtracted from the stored exponent. | |
| − | + | The stored exponents 000002 and 111112 are interpreted specially. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
例子 | 例子 | ||
2019年11月27日 (三) 19:26的版本
目录 |
1 概述
IEEE754 标准是 IEEE 对浮点数表示的规范,目的在于统一浮点数的编码,提高浮点运算程序的可移植性。
IEEE754有3种浮点数格式:单精度、双精度、扩展双精度。
每种格式皆由3部分组成: 符号位(s)、指数(e)和尾数(m)。
single-precision : | 31 | 30:23 | 22:0 | (Ns=1, Ne=8, Nm=23) double-precision: | 63 | 62:52 | 51:0 | (Ns=1, Ne=11, Nm=52) double-extended: | 79 | 78:64 | 63:0 | (以x86之80位为例)
所表示值按指数域分为归一化值和未归一化值。
IEEE754-2008 标准引入了 半精度浮点(Half-Precision Float) float16 类型:'
gcc 中在 arm/AArch64 (64-bit execution state of the ARMv8 ISA) 中支持这个类型 __fp16,ARM 编译时带参数 -mfp16-format=ieee 即可,AArch64 无需此参数。
arm 需包头文件 <arm_fp16.h>,编译是带参数 -mfpu=neon-fp16 -mfloat-abi=softfp
- -mfp16-format=ieee, selects the IEEE 754-2008 format. Normalized values in the range of 2^{-14} to 65504. There are 11 bits of significand precision, approximately 3 decimal digits
- -mfp16-format=alternative, selects the ARM alternative format. Normalized values in the range of 2^{-14} to 131008. Similar to the IEEE format, but does not support infinities or NaNs
2 半精度浮点
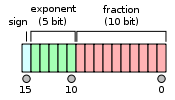
IEEE 754 标准指定了一个binary16要有如下的格式:
- Sign bit(符号位): 1 bit
- Exponent width(指数): 5 bits
- Fraction(尾数): 11 bits (10位显式存储,隐含 1 位)
fraction 为尾数,10 位显式存储,隐含 1 位,尾数可以理解为是一个浮点数小数点后的数,如1.11,尾数就为1100000000(1),最后的隐含1主要用于计算时,隐含1可能存在可以进位的情况。
exponent 为指数位,有 5 位长:
The half-precision binary floating-point exponent is encoded using an offset-binary representation, with the zero offset being 15; also known as exponent bias in the IEEE 754 standard.
- Emin = 000012 − 011112 = −14
- Emax = 111102 − 011112 = 15
- Exponent bias = 011112 = 15
Thus, as defined by the offset binary representation, in order to get the true exponent the offset of 15 has to be subtracted from the stored exponent.
The stored exponents 000002 and 111112 are interpreted specially.
例子
0 01111 0000000000 = 1 0 01111 0000000001 = 1 + 2^−10 = 1.0009765625 (1之后的最接近的数) 1 10000 0000000000 = −2 0 11110 1111111111 = 65504 (max half precision)(-1)^0×2^(30-15)×1.1111111111 = 1.1111111111×2^15,即十进制的65504 0 00001 0000000000 = 2^-14 ≈ 6.10352 × 10^-5 (最小正指数)(-1)^0×2^(1-15)×(1+0.0) 0 00000 1111111111 = 2^-14 - 2^-24 ≈ 6.09756 × 10^-5 (最大尾数) 0 00000 0000000001 = 2^-24 ≈ 5.96046 × 10^-8 (最小正尾数) 0 00000 0000000000 = 0 1 00000 0000000000 = -0 0 11111 0000000000 = infinity 1 11111 0000000000 = -infinity 0 01101 0101010101 = 0.333251953125 ≈ 1/3
import the file "ieeehalfprecision.c" into your project and use it like this :
float myFloat = 1.24; uint16_t myfp16; float2halfp(&myfp16, &myFloat, 1); // it accepts a series of floats, so use 1 to input 1 float // an example to revert the half float back float myfp32; halfp2float(&myfp32, &myfp16, 1);
3 归一化值
当 e != 0 && e != ~0 (全0与全1)所表示值为归一化值
V = (-1)^s * 2^E * (M+1)
其中 E = e - Bias, Bias = 2^(Ne-1)-1
如单精度浮点数 Bias = 127, V = (-1)^s * 2^(e-127) * (M+1)
4 未归一化值
当 e == 0 || e == ~0 时,所表示值为未归一化值
- 1. e == 0
m == 0, s == 0 ---> +0.0 m == 0, s == 1 ---> -0.0 m != 0 则V = (-1)^s * 2^E * M,其中E = 1 - Bias, Bias = 2^(Ne-1)-1
如单精度浮点数的话,e==0, m!=0, 则 E = 1-127 = -126
- 2. e == ~0
m == 0, s == 0 ---> +INFINITY m == 0, s == 1 ---> -INFINITY 如果 m != 0 ----> NaN, Not a Number
例1 二进制单精度浮点数转十进制数
0x80480000 1000 0000 0100 1000 0000 0000 0000 0000
1 00000000 10010000000000000000000
s = 1
e = 0, E = 1 - 127 = -126
因e == 0,则:尾数部分M为(无须加1):
0.10010000000000000000000=0.5625
该浮点数的十进制为:
(-1)^1 * 2^(-126) * 0.5625 = -6.612156e-39
可以使用如下 C 程序验证之:
#include <stdio.h>
union FI
{
float f;
struct
{
unsigned char b0;
unsigned char b1;
unsigned char b2;
unsigned char b3;
};
}u;
int main()
{
u.b3 = 0x80;
u.b2 = 0x48;
u.b1 = 0x00;
u.b0 = 0x00;
printf ("x = %e ", u.f);
return 0;
}
更简洁的:
#include <stdio.h>
int main()
{
int x = 0x80480000;
float y = *(float *)&x;
printf ("x = %e ", y);
return 0;
}
5 Reference